运算放大器10个经典电路案例
发布日期:2024-10-14
点击次数:489
运放电路
由运算放大器组成的电路,简称为运放电路。
这些电路可以说是五花八门,是我们学习模拟电子技术的一个重要内容,更是一个电子工程师必须掌握的电路之一。运放电路有多种类型,是不是我们把它们牢牢记住就行了呢?
不是!毕竟电路是会变的,换个套路你如果就不会,这样就没有意义了。正确的打开方式还是应该理解它,消化它。
在分析运放电路工作原理时,首先请忘掉什么同向放大、反向放大,什么加法器、减法器,什么差动输入……暂时忘掉那些输入输出关系的公式……这些只会干扰你,让你更糊涂﹔也请各位暂时不要理会输入偏置电流、共模抑制比、失调电压等电路参数,这是设计者要考虑的事情。我们理解的就是理想放大器,因为理解了理想放大器,多数情况是够用的
现在,通过两招就能解决大部分运放问题,并且,这两招在所有运放电路的教材里都写得明白,就是“虚短”和“虚断”,不过要把它运用得出神入化,就要有较深厚的功底了。
基于这一理论,我们通过4个经典电路,来快速掌握运算的分析方法!
关于虚短和虚断
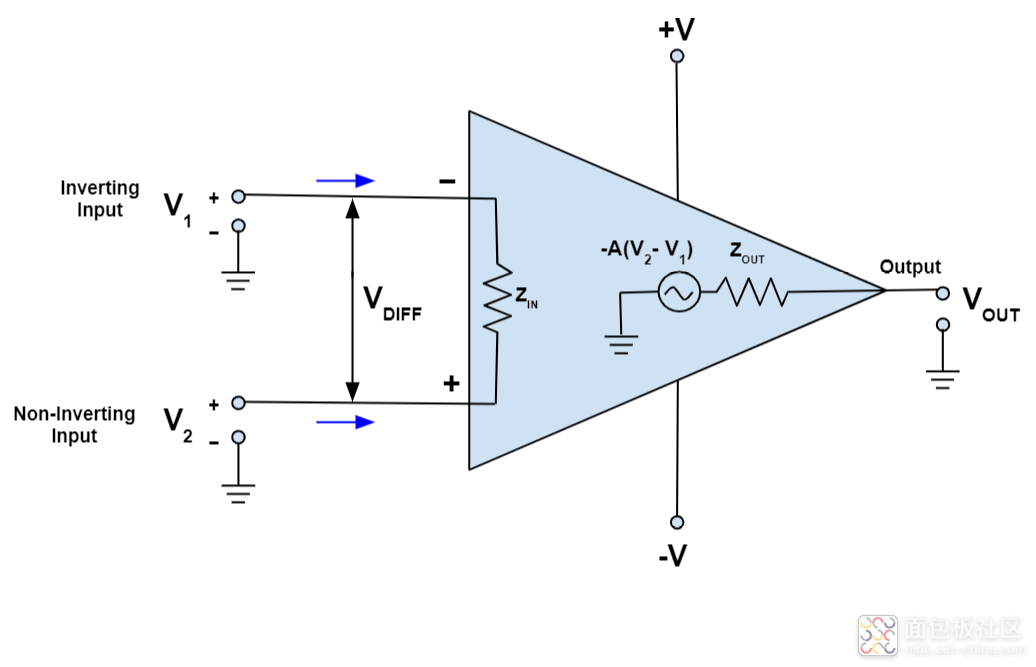
由于运放的电压放大倍数很大,一般通用型运算放大器的开环电压放大倍数都在 80dB 以上。而运放的输出电压是有限的,一般在 10 V~14 V。因此运放的差模输入电压不足 1 mV,两输入端近似等电位,相当于 “短路”。开环电压放大倍数越大,两输入端的电位越接近相等。我们用这样的反推来理解虚短的概念。
“虚短”是指在分析运算放大器处于线性状态时,可把两输入端视为等电位,这一特性称为虚假短路,简称虚短。显然不能将两输入端真正短路。(输入差模电压不大于1mv)
如何理解“虚断”呢?由于运放的差模输入电阻很大,一般通用型运算放大器的输入电阻都在 1MΩ以上。因此流入运放输入端的电流往往不足 1uA,远小于输入端外电路的电流。故通常可把运放的两输入端视为开路,且输入电阻越大,两输入端越接近开路。
“虚断”是指在分析运放处于线性状态时,可以把两输入端视为等效开路,这一特性 称为虚假开路,简称虚断。显然不能将两输入端真正断路。(差模输入电阻无穷大)
好了,概念就介绍到这里,我们来用以上的理论,来分析几个案例,看是否好使?
第一个案例:

由上图,分析如下:
首先,根据虚短,图一运放的同向端接地=0V,反向端和同向端 虚短,所以也是 0V
其次,根据虚断,反向输入端输入电阻很高,虚断,几乎没有电流注入和流出
那么R1和R2相当于是串联的,流过一个串联电路中的每一只组件的电流是相同的,即流过 R1 的电流和流过 R2 的电流是相同的。
流过 R1 的电流 I1 = (Vi - V-)/R1
流过 R2 的电流 I2 = (V- - Vout)/R2
V- = V+ = 0
I1 = I2
求解上面的代数方程
Vout = (-R2/R1)*Vi
这样,我们就设计了一个最经典的反向比例放大器
第二个案例:
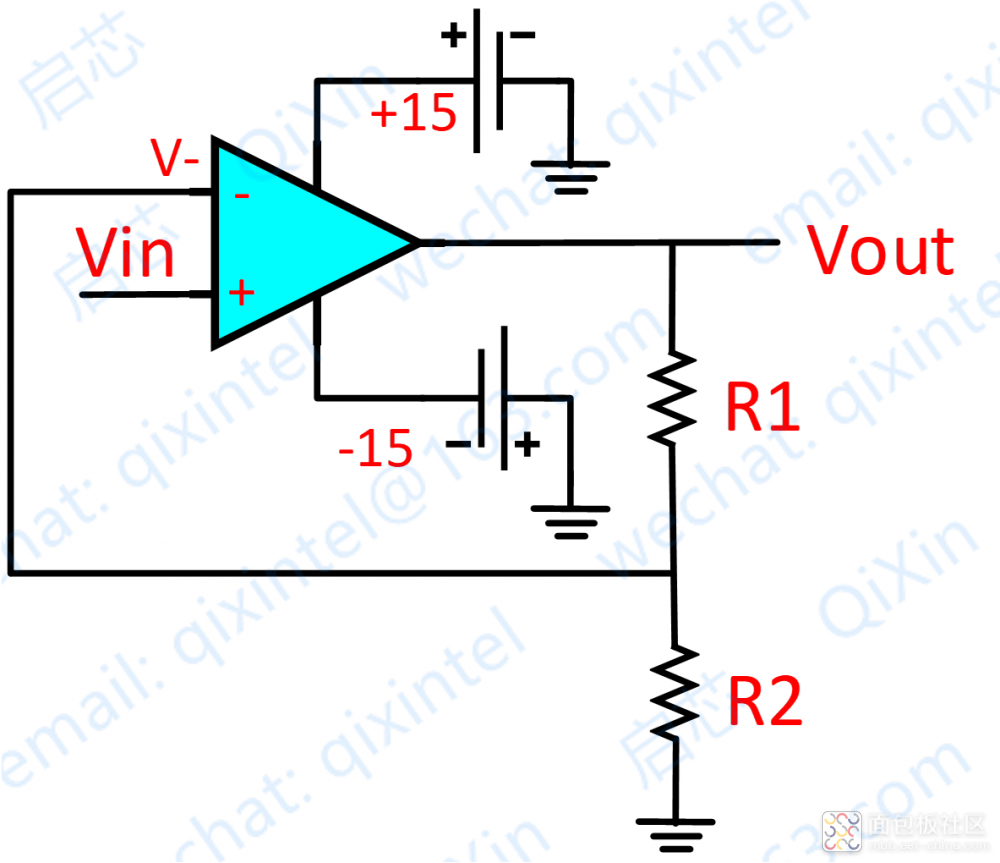
再看上图,分析如下:
Vi 与 V- 虚短,则 Vi = V-
因为虚断,反向输入端没有电流输入输出,通过 R1 和 R2 的电流相等,设此电流为 I
由欧姆定律得:I = Vout/(R1+R2)
Vi 等于 R2 上的分压, 即:Vi = I*R2
由上面式子得
Vout=Vi*(R1+R2)/R2
这样,我们就设计了一个同向放大器。
第三个案例:
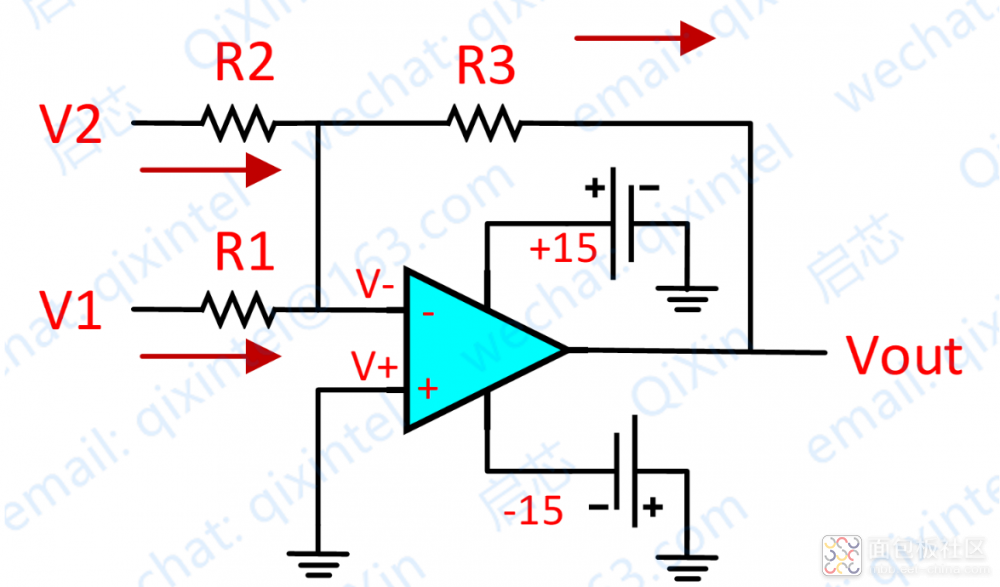
再看上图,分析如下:
由虚短知:V- = V+ = 0
由虚断及基尔霍夫定律知,通过 R2 与 R1 的电流之和等于通过 R3 的电流,故 (V1 – V-)/R1 + (V2 – V-)/R2 = (Vout – V-)/R3
联立上面两个式子很容易得到 V1/R1 + V2/R2 = Vout/R3
如果存在 R1=R2=R3,则上式变为 Vout=-(V1+V2),
这样,我们就设计了一个加法器啦。
我一直都认为,实践是学习的硬件电路知识最好的方法。但是,动手搭建电路很费时间,而设计原理图打PCB板不仅花时间而且费钱,因此,折衷最好的方法就是仿真了。平心而论,只要模型准确,实际上,仿真的结果是无限接近实际情况的。
况且,通常我们只是工程上设计,判断趋势,知道大体方向与数值即可。并不需要太严谨的结果,因此,从这个方面来说,仿真大多数情况下,用来分析问题,是完全够用的。
对于上面这个案例,我们仿真看看,先看简单的,这个电路和上面的电路唯一不同的是加了平衡电阻
下面是R1=R2=R4的情况,可以看到结果是符合我们预期的,即VO=V1+V2,仿真图例如下
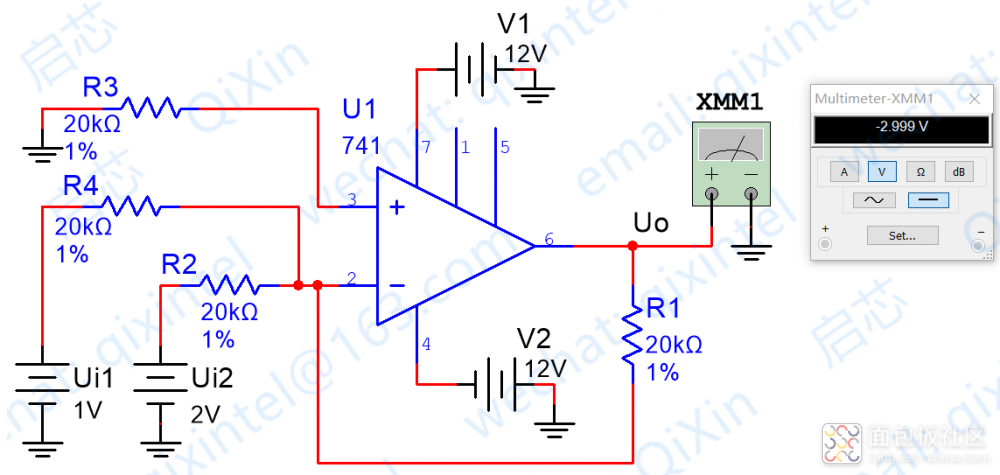
下面是R2=R4 R1=3*R2的情况,可以看到结果也是符合我们预期的,即VO=3*(V1+V2),仿真图例如下
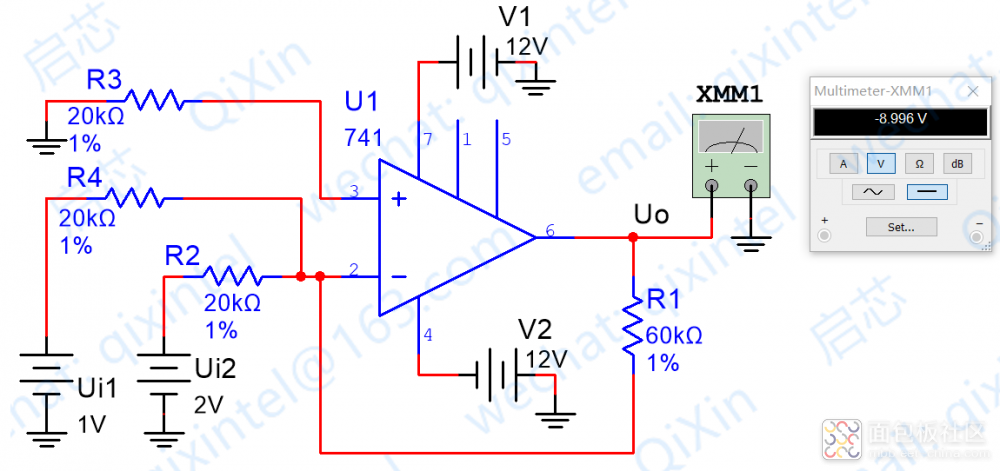
这个电路实际的应用电路,比如用OP07C搭建的低频噪声放大电路,如下图
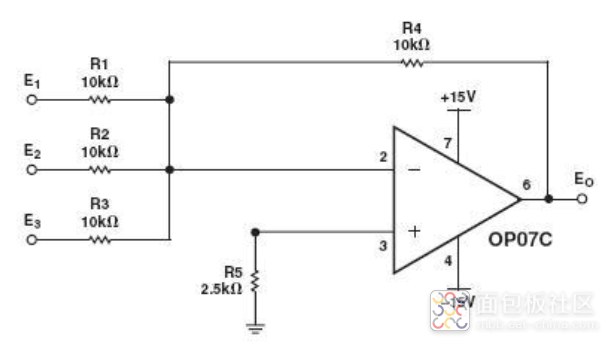
这个电路,比上面讲过的电路稍微复杂,但基本的分析原理是一样的。大家,可以试着计算一下输出公式。
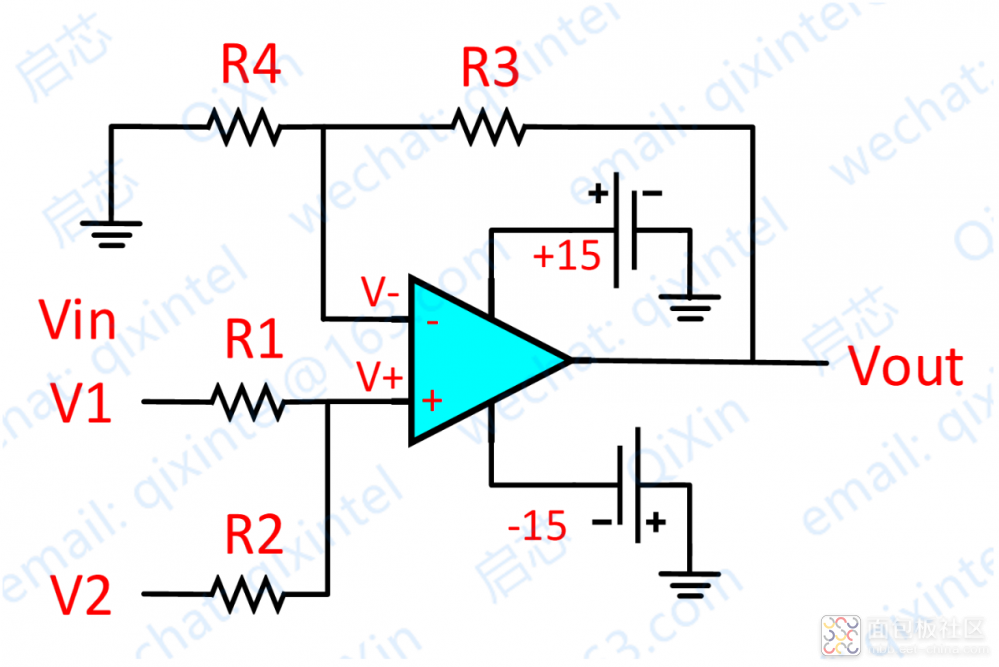
再看上图,分析如下:
因为虚断,运放同向端没有电流流过,则流过 R1 和 R2 的电流相等,同理流过R4和R3的电流也相等。
所以,很容易推出,(V1–V+)/R1 = (V+ - V2)/R2
(Vout – V-)/R3 = V-/R4 ……b
然后,再由虚短知:V+ = V-
如果 存在条件R1=R2,R3=R4,
则由以上式子可以推导出 V+ = (V1 + V2)/2
V- = Vout/2
故 Vout = V1 + V2
这样,我们就设计了一个新的加法器。
由上面四个例子,我们可以看到基本的运算放大器电路,无论电路的形式、连接如何变化,但只要掌握了基本的原理,虚短和虚断,运放的电路基本都可以迎刃而解!
上面讲了运算的一般分析计算方法。
其中,重点提到了运放分析的两把“板斧”——“虚短”和“虚断”,有了这两个基本概念,再结合常用的欧姆定律,基尔霍夫电流,电压定律基本就可以解决大多数问题了。
我们现在可以用这个工具进行更复杂的电路的分析了。
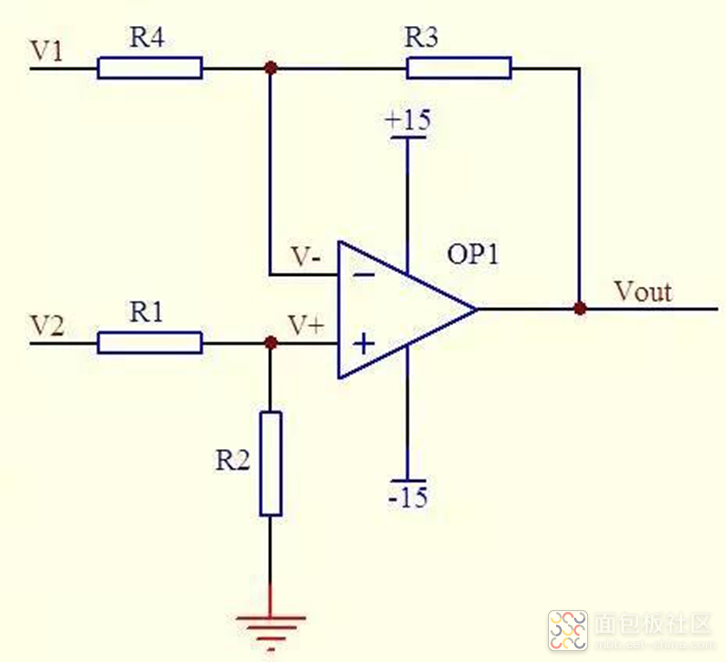
先看上图,分析如下:
由虚断知,通过R1的电流等于通过R2的电流,同理通过R4的电流等于R3的电流,故有 (V2 – V+)/R1 = V+/R2
(V1 – V-)/R4 = (V- - Vout)/R3
如果 R1=R2, 则 V+ = V2/2
如果 R3=R4, 则 V- = (Vout + V1)/2
由虚短知 V+ = V-
所以 Vout=V2-V1
这样,我们就设计了一个新的减法器了。

再看上图,分析如下:
由虚短知,反向输入端的电压与同向端相等
由虚断知,通过R1的电流与通过C1的电流相等。
通过R1的电流 i=V1/R1
通过 C1 的电流 i=C*dUc/dt=-C*dVout/dt
所以 Vout=((-1/(R1*C1))∫V1dt
输出电压与输入电压对时间的积分成正比
这样,我们就设计了一个新的积分电路了。
若 V1 为恒定电压 U,则上式变换为 Vout = -U*t/(R1*C1) t 是时间,则 Vout 输出电压是一条从 0 至负电源电压按时间变化的直线。
对于上面这个电路,对于新手来说,不太好理解,那我们也可以简单仿真分析一下。
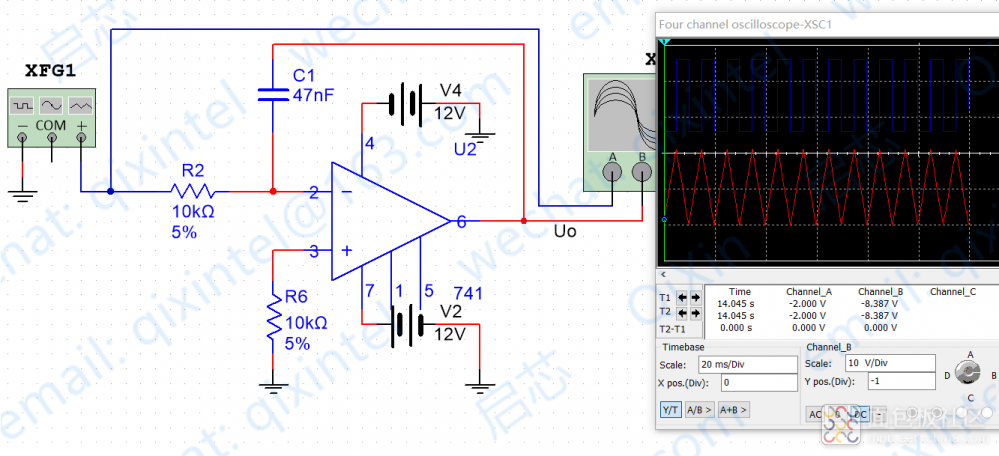
首先,来搭建一个积分电路
如下图,仿真结果在右边,对着图形分析就比较容易了。示波器上面蓝色的方波是信号发生器产生的,下面的锯齿波就是通过积分电路后的波形。
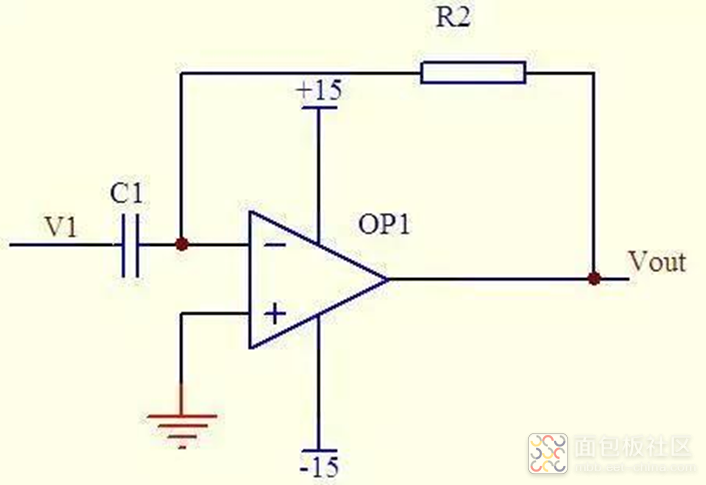
再看上图,分析如下:
图中由虚断知,通过电容 C1 和电阻 R2 的电流是相等的
由虚短知,运放同向端与反向端电压是相等的。
所以有:Vout = -i * R2 = -(R2*C1)dV1/dt
因此,我们这里设计了一个微分电路。
如果 V1 是一个突然加入的直流电压,则输出 Vout 对应一个方向与 V1 相反的脉冲。
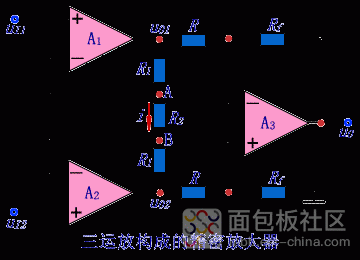
为了获得高共模抑制比,一般取Rf=R,然后根据电压增益选择R1、R2。
电压增益A=1+2R1/R2
电压增益定了,R2也定了,就可以根据R2定制R1
电路的详细分析如下:
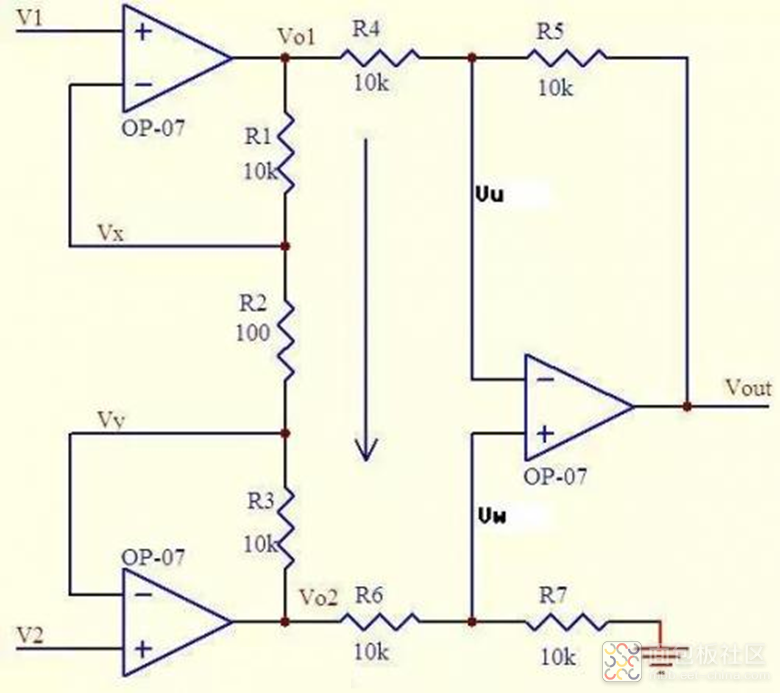
再看上图,分析如下:
上图中,由虚短知 Vx = V1 Vy = V2
由虚断知,运放输入端没有电流流过,则 R1、R2、R3 可视为串联,通过每一个电阻的电流是相同的, 电流 I=(Vx-Vy)/R2
则:Vo1-Vo2=I*(R1+R2+R3) = (Vx-Vy)(R1+R2+R3)/R2
由虚断知,流过 R6 与流过 R7 的电流相等,若 R6=R7,则Vw = Vo2/2
同理若 R4=R5,则 Vout – Vu = Vu – Vo1,故 Vu = (Vout+Vo1)/2
由虚短知,Vu = Vw
由以上三式子很容易得到 Vout = Vo2 – Vo1
进而可以求得 Vout = (Vy –Vx)(R1+R2+R3)/R2 上式中(R1+R2+R3)/R2 是定值,此值确定了差值(Vy –Vx)的放大倍数。
这样,就设计了一个差分放大电路了。
再看上图,分析如下:
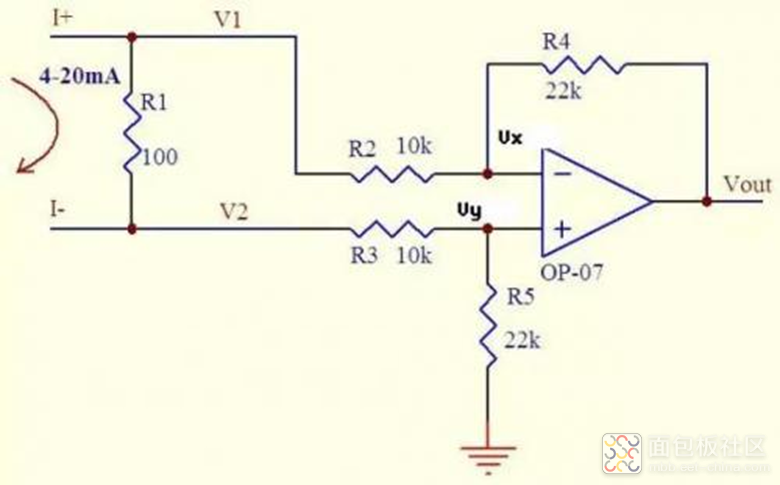
很多控制器接受来自各种检测仪表的 0~20mA 或 4~20mA 电流,电路将此电流转换成电压后再送 ADC 转换成数字信号
上图就是这样一个典型电路。
如图 4~20mA 电流流过采样 100Ω电阻 R1,在 R1 上会产生 0.4~2V 的电压差。
由虚断知,运放输入端没有电流流过,则流过 R3 和 R5 的电流相等,流过 R2 和 R4 的电流相等。
故:(V2-Vy)/R3 = Vy/R5 (V1-Vx)/R2 = (Vx-Vout)/R4
由虚短知:Vx = Vy
电流从 0~20mA 变化,则 V1 = V2 + (0.4~2)
由上面式子代入得(V2 + (0.4~2)-Vy)/R2 = (Vy-Vout)/R4
如果 R3=R2,R4=R5,
则得到 Vout = -(0.4~2)R4/R2
图中 R4/R2=22k/10k=2.2,
则式 Vout = -(0.88~4.4)V,即是说,将 4~20mA 电流转换成了 -0.88 ~ -4.4V 电压,此电压可以送 ADC 去处理。完整的过程就是这样的
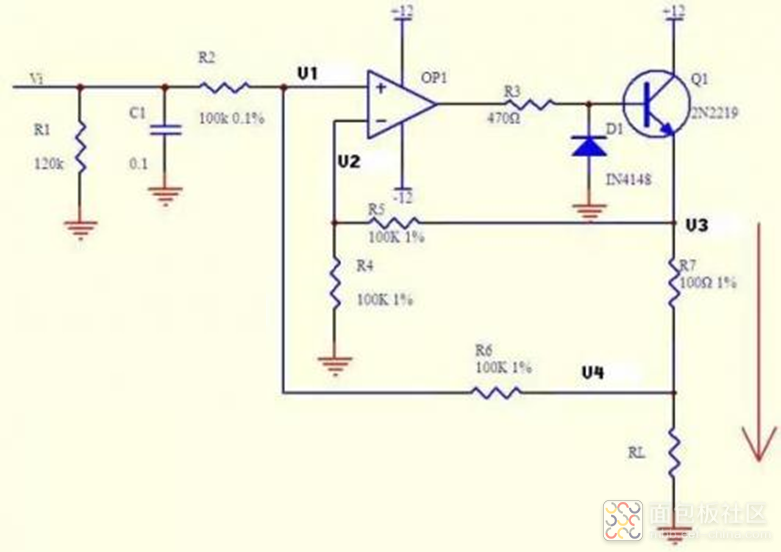
再看上图,分析如下:
电流可以转换成电压,电压也可以转换成电流。
上图的负反馈没有通过电阻直接反馈,而是串联了三极管 Q1 的发射结,不要以为是一个比较器。
只要是放大电路,虚短虚断的规律仍然是符合的!
由虚断知,运放输入端没有电流流过,
则 (Vi – V1)/R2 = (V1 – V4)/R6
同理 (V3 – V2)/R5 = V2/R4
由虚短知 V1 = V2
如果 R2=R6,R4=R5,则由式得 V3-V4=Vi
上式说明 R7 两端的电压和输入电压 Vi 相等,则通过 R7 的电流 I=Vi/R7,如果负载 RL<<100KΩ,则通过 Rl 和通过 R7 的电流基本相同。
我们分析了将近10个运放的电路,并且部分电路通过仿真进一步分析,可以看出,只要掌握了正确的方法,更复杂的电路也可以一步一步的分析出来。
声明:
本文部分信息来源于网络,如有问题请联系,谢谢










